Üslü Sayılarda özellikleri gösterme

Üs Kavramı:

(a)          reel sayı ve (m) bir pozitif tamsayı olmak üzere; a^m  ifadesi, m tane (a) nın çarpımını gösterir.

a^m = a . a . a...a şeklinde gösterilir.

Örnekler:

2³ = 2 . 2 . 2 =8

5² = 5 . 5 = 25

Özellikler:

·    Sıfırdan farklı bir sayını sıfırıncı kuvveti 1’e eşittir.

a^m = a⁰ = 1

Örnekler:  3⁰ = 1

·    Bir sayının birinci kuvveti kendisine eşittir.

a^m = a¹ = a

Örnekler:  2¹ = 2

·    Bir kesrin kuvvetini almak için pay ve paydasının ayrı ayrı kuvvetleri alınır.

( a )^m = a^m

b         b^m

Örnekler: ( 2 )⁵ = 2⁵ = 32

3         3⁵    243

·    Üslü bir ifadenin kuvveti alınırken üsler çarpılır.

(a^m)ⁿ = a^{m . n}

Örnekler: ( 2³)² = 2^{3 . 2} = 2⁶ = 2 . 2 . 2 . 2 . 2 . 2 = 64

·    a ¹ 0 reel sayı ve m bir pozitif tamsayı için;

a^-m = 1

a^m

Örnekler:  2³  = 1   =  1

2³      8

·    Bir kesrin üssü negatif ise kesir ters çevrilip üssü pozitif yapılır.

( a )^-m = ( b )^m

b             a

Örnekler:   ( 2 )^-3 = ( 3 )³ =27

3             2        8

Tek veya Çift Kuvvetler:

(-2)⁴ = (-2) .(-2) . (-2) . (-2) = +16

Sıfırdan farklı bir sayının;

·    Çift kuvvetleri pozitiftir.

·    Tek kuvvetleri ise bu sayı ile aynı işaretlidir.

Üslü İfadelerde Toplama ve Çıkarma:

Tabanları ve üsleri aynı olan ifadelerin katsayıları toplanır ya da çıkarılır.

Örnek

Örnek: 3a⁵ –8a⁵  + a⁵ toplamının sonucu nedir?

Çözüm: a⁵ ’lerin katsayılarını toplayalım.

(3-8+1) a⁵  = 4a⁵

Üslü İfadelerde Çarpma:

·    Tabanları aynı üsleri farklı olan üslü ifadeler çarpılırken ortak taban, taban olarak alınır. Üsler toplanıp üs olarak yazılır.

a^m . aⁿ = a^m+n

·    Tabanları farklı üsleri aynı olan üslü ifadeler çarpılırken tabanlar çarpılıp taban olarak yazılır ortak üs, üs olarak yazılır.

a^m . b^m = (a+b)^m

·    Tabanları ve üsleri farklı molan üslü ifadeler çarpılırken, önce kuvvetler alınır sonra çarpma işlemi yapılır.

Örnek: 2³ . 5² =  8 . 25 = 200

Çarpma işlemi için 2 durum vardır.

a) Tabanları aynı üsleri farklı ise aynı tabanda yazılıp üsleri toplanır.

x Î R , n, m Î Z için   x^m . xⁿ = xⁿ   dir.

b) Tabanları farklı üsleri aynı ise; tabanlar çarpılır üslerden biri ortak üs olarak yazılır.

x, y Î R , n Î Z için   xⁿ . yⁿ = (x . y) ⁿ dir.

Örnek

2⁹⁹ . 5⁹⁹ = (2.5) ⁹⁹  =  10⁹⁹

2⁷ . 3⁷ . 5⁷ = (2.3.S) ⁷ = 30⁷   dir.

(a + b) ³ . (a - b) ³ = [ (a+b) (a-b) ] ³ = (a² - b²) ³ Başka bir örnekte tersten de düşünürsek

42 ^X = (2.3.7) ^X = 2 ^X . 3 ^X . 7 ^X   olur.

Bir uslu sayının kuvvetinin kuvveti var ise aynı tabanda kuvvetler çarpılır.

x Î R ,   m, n Î Z için   (xⁿ)m = (x^m) ⁿ = x^m.n dir.

Örnek

(5³) ^2x = 5^6x dir.

Bunun değişik versiyonlarını elde edebiliriz.

(5³) ^2x = (5 ^X)6 = (5²) ^3x = (5⁶) ^X = (5^2X) ³ = (5^6x) gibi.

Örnek

Örnek

Üslü İfadelerde Bölme:

·    Tabanları aynı üsleri farklı olan üslü ifadeler bölünürken ortak taban, taban olarak alınır, üsler çıkarılıp üs olarak yazılır.

a^m  = a^{m – n}

aⁿ

Örnekler: 2⁸  = 2^8-5 = 2³ = 8

2⁵

·    Tabanları farklı üsleri aynı üslü ifadeler bölünürken; tabanlar bölünüp taban olarak alınır. Ortak üs üs olarak yazılır.

Örnekler: ( 81 )⁴ = 3⁴ = 81

27

·    Tabanları ve üsleri farklı olan üslü ifadeler bölünürken tabanlar bölünüp önce kuvvetler açılır sonra bölme işlemi yapılır.

Üslü Denklemler:

Üssünde bilinmeyen bulunan denklemlere üslü denklemler denir.

Örnek: 9^{2x – 3} = 27^{x –1} ise   x’i bulalım.

Çözüm: (3²)^{2x – 3} = (3³)^{x – 1}

4x – 6 = 3x - 3

x =  3 bulunur.

Çözüm

Örnek

7^3x-15 = 1  ise   x   nedir?

Çözüm

7^3x-15 = 1  =  7

3x-15 = 0

3x= 15

x = 5    olur.

2)

a) m tek ise; .x = y

b) m çift ise; x = + y   dır.

Örnek

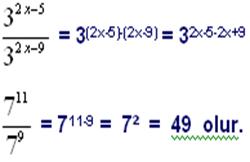
Örnek

10’un Kuvvetleri

a) n Î N⁺ olmak üzere

10 ⁿ = 1 00... 0’dır.

10 ⁿ sayısında n tane sıfır vardır ve sayı (n + 1) basamaklıdır.

b) n Î N olmak üzere

10^-n sayısında virgülün sağında (n-1) tane sıfır ve n tane rakam vardır.

Örnek

700000000 = 7.10⁸ = 70.10⁷ = 700.10⁶   gibi değişik şekillerde yazılabilir.

0,00015=15.10^-5=1,5.10^-4=0,15.10^-3=150.10^-6 gibi değişik şekillerde de yazabiliriz.

Çözümlü Test

1. 3 ^X+1 - 5.3 ^X + 7.3 ^X + 3 ^X = 54 ise x kaçtır?

A) 2      B) 3          C) 4          D) 6          E) 8

Çözüm

3 ^X. 3 - 5.3 ^X + 7.3 ^X + 3 ^X = 54

(3-5 + 7 + 1).3 ^X = 54

6.3 ^X = 54

3 ^X = 9 = 3²

x - 2   dir.

Cevap : A

Çözüm

3.

işleminin sonucu nedir?

A) -4        B) -2        C) 2 D) 4          E) 5

Çözüm

Cevap : C

4.

işleminin sonucu kaçtır?

Çözüm

5. 3.2 ^x+z + 4.2 ^x = 8 olduğuna göre x kaçtır?

A) 2         B)1          C) O         D)-1        E)-2

Çözüm

Cevap: D

6.

olduğuna göre  a.b  çarpımı kaçtır?

A) 12        B) 24       C) 36       D) 48       E) 60

Çözüm

Cevap :  D

7. (2^-1 + 2°)^-2. 3² işleminin sonucu kaçtır?

A) 2      B) 3          C) 4          D) 5          E) 6

Çözüm

Cevap: C

8.

olduğuna göre a kaçtır?

Çözüm

Cevap : C