Kartezyen çarpım :
İlk elemanı birinci kümeden , ikinci elemanı ikinci kümeden gelen ikililerin oluşturduğu kümeye denir.
Örnek 1: A = {1,2,3} ve B = {a,b} ise
AxB = {(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)} olur.
BxA = {(a,1),(b,1),(a,2),(b,2),(a,3),(b,3)} şeklinde yazılır.
Örnekte görüldüğü gibi
( kartezyen çarpım işleminde değişme özelliği yoktur ).
Yine örnekte görüldüğü gibi A kümesinin 3 , B kümesinin 2 elemanı vardır. AxB kümesinin eleman sayısı ise 6 ‘dır. Böyle olması tesadüf değildir.
Çünkü kartezyen çarpım kümesinin eleman sayısı ; kartezyen çarpımı oluşturan kümelerin eleman sayılarının çarpımına eşittir.
Aynı sebeple BxA kümesinin eleman sayısı da 6 ‘dır. Yani kartezyen çarpım işleminde değişme özelliği olmamasına karşılık her kümenin eleman sayıları eşittir ( Denk kümeler ).
( kartezyen çarpım işleminde değişme özelliği yoktur )
s(AxB) = s(BxA) = s(A) s(B) ( Denk kümeler )
BAĞINTI
Kartezyen çarpım kümesinin herhangi bir alt kümesine denir. Eğer bağıntı, AxB ‘nin alt kümesi ise o bağıntıya A’dan B’ye bir bağıntı denir. Buradaki birinci küme, bağıntının tanım kümesi ; ikinci küme ise bağıntının değer kümesi olarak adlandırılır.
“n” elemanlı bir kümenin tüm bağıntılarının sayısı 2n olduğundan dolayı A’dan B’ye yazılabilecek tüm bağıntıların sayısı da 2s(A)s(B) ‘ dir.
Örnek 2: s(A) = 5 ve s(B) = 4 ise A’dan B’ye yazılabilecek tüm bağıntıların sayısı 220 olur. Tabii ki aynı şekilde B’den A’ya yazılabilecek tüm bağıntıların sayısı da 220 ‘dir.
Örnek 3 : A = {1,2,3} ve B = {1,2,a,b} olmak üzere A’dan B’ye bir bağıntı tanımlayalım :
={(1,1),(2,1),(2,2),(3,a) } ise grafik ile gösterimi şöyle olur :

: A B olmak üzere tanımlanmış bağıntının tanım kümesi A,
değer kümesi B, görüntü kümesi ise C ‘dir.
NOT : : A B ( A’dan B’ye bir bağıntıdır diye okunur)
C = (A) = { (1), (2), (3)} = {1,2,a} kümesine görüntü kümesi denir ve her zaman değer kümesi ile aynı anlama gelmeyebilir.
Örnek 4 : s(A) = 4 olduğuna göre A’ dan A’ya yazılabilecek bağıntıların kaç tanesi 3 elemanlıdır ?
Çözüm : s(AxA) = 16 olduğundan ve 16 elemanlı bir kümenin 3 elemanlı alt kümelerinin sayısı
Örnek 5 : A={a,b,c,d} kümesi üzerinde tanımlanan
={(a,a),(a,c),(b,c),(b,d),(c,d)} bağıntısını grafik ile gösteriniz :
Çözüm :
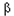
Bağıntıların özellikleri :
1. Yansıma özelliği : Bir A kümesi üzerinde tanımlanan bağıntı , A kümesinin tüm elemanları için yazılabilecek (x,x) ikililerini içeriyorsa yansıyandır.
2. Simetri özelliği : Bir bağıntı, (x,y) ikilisini içerirken aynı anda (y,x) ikilisini de içeriyorsa simetriktir.
3. Ters simetri özelliği : Bir bağıntı, (x,y) ikilisini içerirken aynı anda (y,x) ikilisini de içermiyorsa ters simetriktir.
4. Geçişme özelliği : Bir bağıntı, (x,y) ikilisini ve (y,z) ikilisini içerirken aynı anda (x,z) ikilisini de içeriyorsa geçişkendir.
Bağıntı çeşitleri :
1. Denklik bağıntısı : Bir bağıntı ; yansıma, simetri ve geçişme özelliklerine sahipse o bağıntıya denklik bağıntısı denir.
2. Sıralama bağıntısı : Bir bağıntı ; yansıma, ters simetri ve geçişme özelliklerine sahipse o bağıntıya sıralama bağıntısı denir.
Örnek 6: A = {1,2,3,4} kümesi üzerinde tanımlanan
= {(1,1),(2,2),(1,2),(3,3),(4,4)} bağıntısının özelliklerini inceleyelim :
Çözüm :
A kümesinin tüm elemanları için (x,x) ikililerini içerdiği için yansıyan,
(1,2) ikilisinin tersi olan (2,1) ikilisini içermediğinden ters simetrik,
(1,1) ve (1,2) varken (1,2) ikilisini de olduğundan geçişkendir.
Bu 3 özelliğin sonucu olarak da sıralama bağıntısıdır.
Örnek 7: A = {1,2,3,4} kümesi üzerinde tanımlanan
= {(1,1),(2,2),(1,2),(2,1),(3,3),(4,4)} bağıntısının özelliklerini inceleyelim :
Çözüm :
A kümesinin tüm elemanları için (x,x) ikililerini içerdiği için yansıyan,
(1,2) ikilisinin tersi olan (2,1) ikilisini içerdiğinden simetrik,
(2,1) ve (1,2) varken (1,1) ve (2,2) ikilisini de olduğundan geçişkendir.
Bu 3 özelliğin sonucu olarak da denklik bağıntısıdır.
Örnek 8: A = {1,2,3,4} kümesi üzerinde tanımlanan
= {(1,1),(2,2),(3,3),(4,4)} bağıntısının özelliklerini inceleyelim :
Çözüm : Yansıyan, simetrik, ters simetrik ve geçişkendir.
Tüm özellikleri sağlamasının sonucu olarak da hem denklik hem de sıralama bağıntısıdır.
Bir bağıntı aynı anda hem simetrik hem de ters simetrik olabilir.
Örnek 9: A = {1,2,3,4} kümesi üzerinde tanımlanan
= {(1,1),(2,2),(1,2),(2,1),(1,3),(4,4)} bağıntısının özelliklerini inceleyelim :
Çözüm :
(3,3) ikilisini içermediği için yansıyan değil ;
(1,3) ikilisinin tersi olmadığı için simetrik değil ;
aynı anda hem (1,2) hem de (2,1) ikililerini içerdiği için ters simetrik değil ; (2,1) ve (1,3) varken (2,3) olmadığından dolayı da geçişken değildir.
Bir bağıntı aynı anda hem simetrik hem de ters simetrik olmayabilir.
Örnek 10: A = {1,2,3,4} kümesi üzerinde tanımlanan
= {(1,1),(2,2),(1,2),(2,1)} bağıntısının özelliklerini inceleyelim :
Çözüm :
(3,3) ve (4,4) ikililerini içermediği için yansıyan değil ;fakat simetrik ve geçişkendir.
: A ® A ve s(A) = n olmak üzere
Tanımlanabilen bağıntı sayısı  ;
;
Tanımlanabilen yansıyan bağıntı sayısı  ;
;
Tanımlanabilen simetrik bağıntı sayısı  ‘ dir.
‘ dir.





0 yorum :
Lütfen Yorumunuzun anlaşılır ve imla kurallarına uygun olmasına dikkat ediniz.